
I recently heard a question referring to the “pathfinding problem” which I found fascinating due to the multiple layers of complexity involved. In this article, I explain the problem statement and describe my solution while distilling the problem, which reads:
A player faces a grid board game with multiple coins. At random, a number K of coins will be selected. Find the expected number of steps the player will need to take to collect all coins. The player may start at any coin and can only move up, down, right or left. All coins are guaranteed to be reachable from all other coins.”
Let’s draw an example
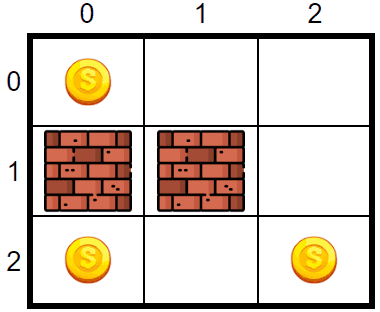
In this scenario, the board is a 3x3 grid. There are three coins located at (0,0), (2,0) and (2,2). If K=2, the game could pick 2 coins in three ways (). These are:
| Coins | Steps required |
|---|---|
| (0,0), (2,0) | 6 |
| (0,0), (2,2) | 4 |
| (2,0), (2,2) | 2 |
Thus, the expected number of steps in this board with is
Reframing
Changing the focus of the problem from a map traversal to a graph traversal should help when thinking about solutions. If we think of coins as nodes, the edges are the shortest path from one coin to the other, each map can be represented as an undirected weighted graph.
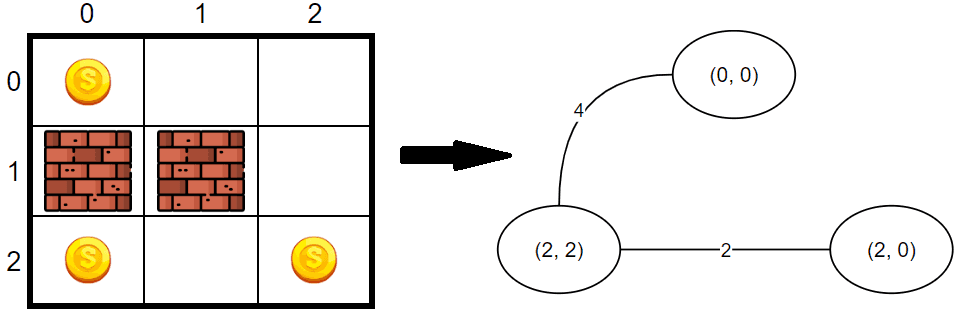
Now, for convenience, we could transform this graph into a fully connected variant by calculating the shortest path for every pair of nodes
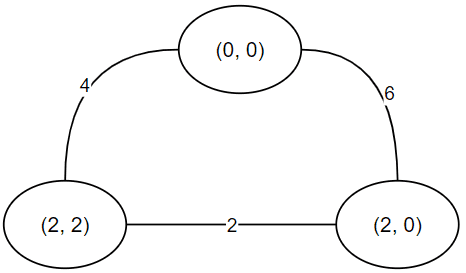
In most cases, we won’t work with the full map but with a subset of it, which continues to be a fully connected undirected weighted graph.
Framing the problem this way unveils the statement is, at its core, representing a variant of the Travelling Salesman Problem (TSP). In this NP-Hard problem, one has to find the shortest path to visit all nodes and go back to the original node by visiting each exactly once.
The best-known exact solution to the TSP is the Held-Karp Algorithm which runs in , where is the number of nodes. At such complexity, the algorithm becomes impractical at even small .
Thus, we’ll code an approximation, a trimmed deep nearest neighbour algorithm.
Nearest neighbour
Nearest neighbours work by simply following the edge that has the smallest weight, hoping it will lead to the shortest path.
As one can imagine, it is easy to fool an algorithm this short-sighted. To allow it to plan further down, we add a depth parameter to also examine the neighbours of our neighbours, up to level . The algorithm will follow the neighbour with the smallest total cost.
The algorithm’s reliability grows the deeper we allow it to go, nevetheless, its complexity also grows, exponentially. The good news is that not all nodes will need to be evaluated, as some paths will show early signs of being suboptimal.
I find this concept easier to understand if we visualize the search as a tree. I'll use a slightly bigger graph to demostrate.
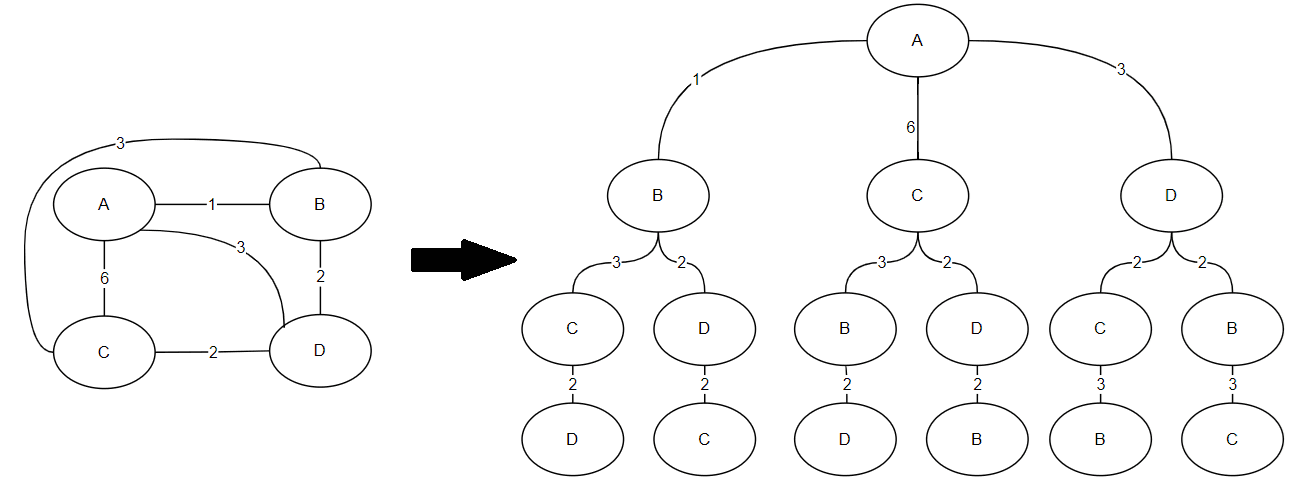
The first clue is that the last level of an undirected the graph will always add the same distance, regardless of being in the left or right branch.
Then, notice that if we start exploring a branch and its subtotal is more than the total of another branch, we can trim the branch completely.
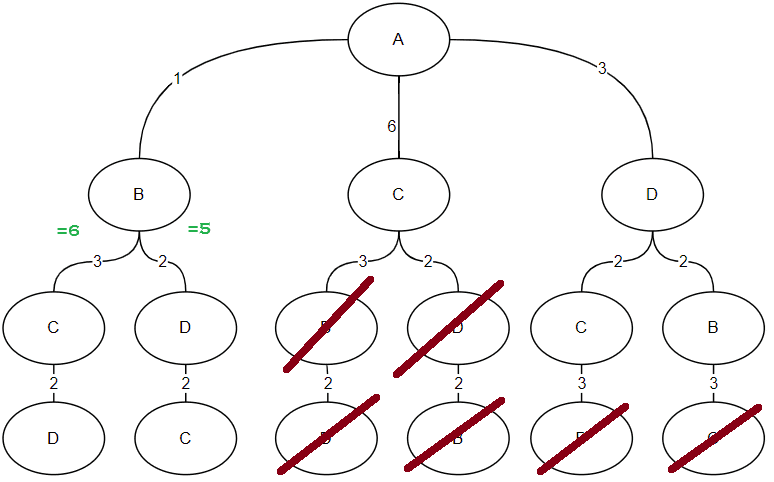
Alright, that’s all the theory. Let’s code.
Set up
First, we need a way to represent the board. This comes as a list of strings where each character in the string represents a field type. . is a space the agent can walk into, * is a coin and # is a wall (thus the agent can’t step into it). For example
*..
#.#
.*.This representation is sufficient as it allows us to access a cell in the grid by indexing twice board[row][column].
We also need a function to find the legal movements an agent can perform from a given position.
def get_movements(position: tuple[int, int], board: list[str]) -> list[tuple[int, int]]:
"""
Get the possible movements from a given position.
"""
movements = []
for row_offset, col_offset in ((1, 0), (0, 1), (-1, 0), (0, -1)):
new_row = position[0] + row_offset
is_row_out_of_bounds = new_row < 0 or new_row >= len(board)
if is_row_out_of_bounds:
continue
new_col = position[1] + col_offset
is_col_out_of_bounds = (
new_col < 0 or new_col >= len(board[0]) or board[new_row][new_col] == "#"
)
if is_col_out_of_bounds:
continue
movements.append((new_row, new_col))
return movementsFor ease of use, let’s encapsulate the concept of a Coin in its own class and allow an attribute to record how far this coin is from the other coins.
class Coin:
def __init__(self, coords: tuple[int, int], i: int) -> None:
self.coords = coords
self.i = i
self.step_distance: dict[tuple[int, int], int] = {}
def __eq__(self, other: "Coin") -> bool:
return self.coords == other.coords
def set_step_distance(self, coords: tuple[int, int], distance: int) -> None:
self.step_distance[coords] = distance
def get_step_distance(self, coords: tuple[int, int]) -> int:
return self.step_distance[coords]Finally, I added some test cases, which are available on GitHub.
Finding the optimal path from A to B
There are many known algorithms to find a path from cell A to cell B in a grid, including Breadth First Search, Best First Search, and Dijkstra’s Search. In this case, I’m implementing A* due to its stability and speed.
def find_path_len_with_a_star(
a: tuple[int, int],
b: tuple[int, int],
board: list[str],
) -> int:
# Keep track of the distance from each cell to a (the original cell)
n_movements = {a: 0}
open = [a] # Cells that need to be explored
close = [] # Cells that have already been explored
while open: # While there are cells to explore
node = open.pop()
next_move_distance = n_movements[node] + 1 # Each move costs 1
close.append(node) # Mark the cell as explored
# Find the valid movement that is closest to b (the goal) according to the euclidean distance
movements = get_movements(node, board)
movements = sorted(movements, key=lambda x: get_euclidean_distance(b, x))
# If we reach the goal in this movement, congrats! Return the distance
if b == movements[0]:
return next_move_distance
# Otherwise, add the next movements to the open list if not already explored
for movement in movements:
n_movements[movement] = next_move_distance
if movement in close or movement in open:
continue
open.append(movement)
# If we got here, there is no path
raise ValueError("No path!")
def get_euclidean_distance(a: tuple[int, int], b: tuple[int, int]) -> float:
return ((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2) ** (1 / 2)We now can fill in the weights of all edges in the graph.
def set_coin_distances(coins: list[Coin], board: list[str]) -> None:
for idx, coin_a in enumerate(coins):
for coin_b in coins[idx + 1 :]:
distance = find_path_len_with_a_star(coin_a.coords, coin_b.coords, board)
coin_a.set_step_distance(coin_b.coords, distance)
coin_b.set_step_distance(coin_a.coords, distance)Traversing the graph with Nearest Neighbours
Now that we know the cost (and the best path) of moving from one coin to another, let’s find the minimum cost of collecting all coins given that we start at a particular coin.
def traverse_graph_with_nn(
current: Coin,
remaining: list[Coin],
depth=1,
best_distance=float("inf"),
) -> int:
"""
Use Nearest Neighbours algorithm to traverse the graph and approximate the
shortest distance that collects all remaining coins.
"""
distance = 0
while len(remaining) > 1:
# Find the nearest neighbour
min_idx = 0
min_distance = float("inf")
min_step_distance = min_distance
for idx, node in enumerate(remaining):
node_distance = node.get_step_distance(current.coords)
if node_distance >= best_distance:
continue
sub_distance = 0
if depth > 1 and len(remaining) > 1:
# Recurse until we've exhausted the depth or the graph
sub_distance = traverse_graph_with_nn(
current=node,
remaining=remaining[:idx] + remaining[idx + 1 :],
depth=depth - 1,
best_distance=min_step_distance,
)
step_distance = node_distance + sub_distance
if step_distance < min_step_distance:
# Update the nearest neighbour
min_step_distance = step_distance
min_distance = node_distance
min_idx = idx
distance += min_distance
current = remaining.pop(min_idx)
if remaining:
distance += remaining[0].get_step_distance(current.coords)
return distance # type: ignoreFinding the shortest distance
We now have all the components necessary to approximate a solution to the problem. Since our method for finding the shortest path across all nodes in the graph is dependent on the starting node, we must execute the search for each potential starting location. Additionally, because the objective is to determine the expected length of a subset of K nodes in our primary graph, we must calculate the optimal distance for each combination of K nodes.
def get_expected_length(board: list[str], K: int) -> float:
# Isolate the coins from the board
coins = []
for row_idx, row in enumerate(board):
for column_idx, column in enumerate(row):
if column == "*":
coins.append(Coin((row_idx, column_idx), len(coins)))
# Find the shortest path from each coin to each other
set_coin_distances(coins, board)
# Calculate the distance that collects all subsets of K coins
path_lenghts = []
for combination in combinations(coins, K):
# Traverse the graph and approximate the shortest distance that collects all coins
best_len = min(
traverse_graph_with_nn(
current=combination[idx],
remaining=list(combination[:idx]) + list(combination[idx + 1 :]),
depth=2,
)
for idx in range(K)
)
path_lenghts.append(best_len)
# Calculate the expected distance
return sum(path_lenghts) / len(path_lenghts)Memoizing
While the algorithm works as expected, it has a few layers of redundancy that could be avoided by memoization.
Running the same algorithm for firrent subsets of nodes, starting nodes and levels in the search of nearest neighbours, will repeatedly ask the question “I’m at node A, what node should I visit next if I still have nodes {B…K} left to visit?”. We can make the algorithm faster by caching the answers to those questions by using the node A and the set {B…K} as the keys to our cache.
To represent a state, we use a tuple, where the first element is the index of the node A, and the second element is an integer whose bit representation denotes the nodes that have yet to be visited with 1, and the nodes that do not need to be visited with 0.
class Memo:
def __init__(self, total: int) -> None:
self.total = total
self.base = 1 << total
self.memo = {}
def get(self, coin: Coin, remaining: list[Coin]) -> float | None:
state = self._get_state(coin, remaining)
if state in self.memo:
return self.memo[state]
return None
def _get_state(self, coin: Coin, remaining: list[Coin]) -> tuple[int, int]:
state = self.base
for rem_coin in remaining:
state |= 1 << rem_coin.i
return (coin.i, state)
def set(self, coin: Coin, remaining: list[Coin], distance: float) -> None:
state = self._get_state(coin, remaining)
self.memo[state] = distance
def get_expected_length(board: list[str], K: int) -> float:
...
memo = Memo(len(coins))
path_lenghts = []
for combination in combinations(coins, K):
# Traverse the graph and approximate the shortest distance that collects all coins
best_len = min(
traverse_graph_with_nn(
current=combination[idx],
remaining=list(combination[:idx]) + list(combination[idx + 1 :]),
depth=2,
memo=memo,
)
for idx in range(K)
)
...
def traverse_graph_with_nn(
current: Coin,
remaining: list[Coin],
memo: Memo | None = None,
depth=1,
best_distance=float("inf"),
) -> int:
distance = 0
path = [current]
while len(remaining) > 1:
if memo:
memoized = memo.get(current, remaining)
if memoized is not None:
# If we have already computed the distance, return it
return distance + memoized # type: ignore
...
if memo:
path.append(current)
...
if memo:
memo.set(path[0], path[1:], distance)
return distance # type: ignore
In the case of our “large” map (see test cases). This change is enough to decrease the running time of the algorithm from 200s to 2.5s (>80x)!
Full solution
Check out the full solution at Github